NATIONAL INSTITUTE OF INDUSTRIAL ENGINEERING

PGDIE-42

Industrial Engineering

 Assignment on Product Manufacture:-

Presented By: -

Amit Rana

Roll NO. 108

Vaibhav Jijani

Roll No.99

PGDIE 42

Manufacturing of Spur Gear Using Powder Metallurgy 

INTRODUCTION

Powder Metallurgy is a proven technology to produce high strength gears and tailored gear shapes for both automotive and industrial applications. Advances in powder production, compaction, and sintering combined with unique secondary processing methods have enabled overall part densities above 7.5 g/cm3. These techniques have proven successful in displacing many components from competing technologies in a variety of end user applications. The reason for P/M’s success is its ability to offer the design engineer the required mechanical properties with reduced component cost. At the present time, P/M is successful in many performance areas. Discussed here are three applications that expand the potential for P/M use in additional environments.

Powder metallurgy is the process of blending fine powdered materials, pressing them into a desired shape or form (compacting), and then heating the compressed material in a controlled atmosphere to bond the material (sintering).
The powder metallurgy process generally consists of four basic steps:
(1) powder manufacture, 
(2) powder blending,
(3) compacting, 
(4) sintering. 
Compacting is generally performed at room temperature, and the elevated-temperature process of sintering is usually conducted at atmospheric pressure. Optional secondary processing often follows to obtain special properties or enhanced precision.

DESIGN OF SPUR GEAR

The spur gear is is simplest type of gear manufactured and is generally used for transmission of rotary motion between parallel shafts.  The spur gear is the first choice option for gears except when high speeds, loads, and ratios direct towards other options.  Other gear types may also be preferred to provide more silent low-vibration operation.  A single spur gear is generally selected to have a ratio range of between 1:1 and 1:6 with a pitch line velocity up to 25 m/s.  The spur gear has an operating efficiency of 98-99%.  The pinion is made from a harder material than the wheel.  A gear pair should be selected to have the highest number of teeth consistent with a suitable safety margin in strength and wear.   The minimum number of teeth on a gear with a normal pressure angle of 20 degrees is 18.

The preferred number of teeth are as follows

12 13 14 15 16 18 20 22 24 25 28 30 32 34 38 40 45 50 54 60
64 70 72 75 80 84 90 96 100 120 140 150 180 200 220 250

The lines normal to the point of contact of the gears always intersects the centre line joining the gear centres at one point called the pitch point.  For each gear the circle passing through the pitch point is called the pitch circle.  The gear ratio is proportional to the diameters of the two pitch circles.  For metric gears (as adopted by most of the worlds nations) the gear proportions are based on the module.

m = (Pitch Circle Diameter(mm)) / (Number of teeth on gear).

In the USA the module is not used and instead the Diametric Pitch d _pis used

d _p = (Number of Teeth) / Diametrical Pitch (inches)

Profile of a standard 1mm module gear teeth for a gear with Infinite radius (Rack ).
Other module teeth profiles are directly proportion . e.g. 2mm module teeth are 2 x this profile

Terminology - spur gears

• Diametral pitch (d _p )- The number of teeth per one inch of pitch circle diameter.
• Module. (m)- The length, in mm, of the pitch circle diameter per tooth.
• Circular pitch (p)-The distance between adjacent teeth measured along the are at the pitch circle diameter
• Addendum ( h _a )- The height of the tooth above the pitch circle diameter.
• Centre distance (a)- The distance between the axes of two gears in mesh.
• Circular tooth thickness (ctt)- The width of a tooth measured along the are at the pitch circle diameter.
• Dedendum ( h _f )-The depth of the tooth below the pitch circle diameter.
• Outside diameter ( D _o )- The outside diameter of the gear.
• Base Circle diameter ( D _b ) - The diameter on which the involute teeth profile is based.
• Pitch circle dia ( p )-The diameter of the pitch circle.
• Pitch point- The point at which the pitch circle diameters of two gears in mesh coincide.
• Pitch to back- The distance on a rack between the pitch circle diameter line and the rear face of the rack.
• Pressure angle- The angle between the tooth profile at the pitch circle diameter and a radial line passing through the same point.
• Whole depth.-The total depth of the space between adjacent teeth.

 

Materials used for gears

Mild steel is a poor material for gears as as it has poor resistance to surface loading.   The carbon content for unhardened gears is generally 0.4%(min) with 0.55%(min) carbon for the pinions.  Dissimilar materials should be used for the meshing gears - this particularly applies to alloy steels.  Alloy steels have superior fatigue properties compared to carbon steels for comparable strengths.  For extremely high gear loading case hardened steels are used the surface hardening method employed should be such to provide sufficient case depth for the final grinding process used.

Material	Notes	applications
Ferrous metals
Cast Iron	Low Cost easy to machine with high damping	Large moderate power, commercial gears
Cast Steels	Low cost, reasonable strength	Power gears with medium rating to commercial quality
Plain-Carbon Steels	Good machining, can be heat treated	Power gears with medium rating to commercial/medium quality
Alloy Steels	Heat Treatable to provide highest strength and durability	Highest power requirement. For precision and high precisiont
Stainless Steels (Aust)	Good corrosion resistance. Non-magnetic	Corrosion resistance with low power ratings. Up to precision quality
Stainless Steels (Mart)	Hardenable, Reasonable corrosion resistance, magnetic	Low to medium power ratings Up to high precision levels of quality
Non-Ferrous metals
Aluminium alloys	Light weight, non-corrosive and good machinability	Light duty instrument gears up to high precision quality
Brass alloys	Low cost, non-corrosive, excellent machinability	low cost commercial quality gears. Quality up to medium precision
Bronze alloys	Excellent machinability, low friction and good compatability with steel	For use with steel power gears. Quality up to high precision
Magnesium alloys	Light weight with poor corrosion resistance	Ligh weight low load gears. Quality up to medium precision
Nickel alloys	Low coefficient of thermal expansion. Poor machinability	Special gears for thermal applications to commercial quality
Titanium alloys	High strength, for low weight, good corrosion resistance	Special light weight high strength gears to medium precision
Di-cast alloys	Low cost with low precision and strength	High production, low quality gears to commercial quality
Sintered powder alloys	Low cost, low quality, moderate strength	High production, low quality to moderate commercial quality
Non metals
Acetal (Delrin	Wear resistant, low water absorbtion	Long life , low load bearings to commercial quality
Phenolic laminates	Low cost, low quality, moderate strength	High production, low quality to moderate commercial quality
Nylons	No lubrication, no lubricant, absorbs water	Long life at low loads to commercial quality
PTFE	Low friction and no lubrication	Special low friction gears to commercial quality

---

Equations for basic gear relationships

It is acceptable to marginally modify these relationships e.g to modify the addendum /dedendum to allow Centre Distance adjustments. Any changes modifications will affect the gear performance in good and bad ways...

Addendum	h a = m = 0.3183 p
Base Circle diameter	Db = d.cos α
Centre distance	a = ( d g + d p) / 2
Circular pitch	p = m.π
Circular tooth thickness	ctt = p/2
Dedendum	h f = h - a = 1,25m = 0,3979 p
Module	m = d /z
Number of teeth	z = d / m
Outside diameter	D o = (z + 2) x m
Pitch circle diameter	d = z . m ... (d g = gear & d p = pinion )
Whole depth(min)	h = 2.25 . m
Top land width(min)	t o = 0,25 . m

 Module (m)

The module is the ratio of the pitch diameter to the number of teeth. The unit of the module is milli-metres.Below is a diagram showing the relative size of teeth machined in a rack with module ranging from module values of 0,5 mm to 6 mm

The preferred module values are

0,5    0,8    1     1,25     1,5     2,5     3     4     5     6     8     10   12     16     20     25     32     40     50

 Normal Pressure angle α

An important variable affecting the geometry of the gear teeth is the normal pressure angle.  This is generally standardised at 20^o.  Other pressure angles should be used only for special reasons and using considered judgment. The following changes result from increasing the pressure angle

Reduction in the danger of undercutting and interference Reduction of slipping speeds Increased loading capacity in contact, seizure and wear Increased rigidity of the toothing Increased noise and radial forces

Gears required to have low noise levels have pressure angles 15^o to17.5^o

 Contact Ratio

The gear design is such that when in mesh the rotating gears have more than one gear in contact and transferring the torque for some of the time.   This property is called the contact ratio.  This is a ratio of the length of the line-of-action to the base pitch.   The higher the contact ratio the more the load is shared between teeth.  It is good practice to maintain a contact ratio of 1.2 or greater. Under no circumstances should the ratio drop below 1.1.

A contact ratio between 1 and 2 means that part of the time two pairs of teeth are in contact and during the remaining time one pair is in contact.   A ratio between 2 and 3 means 2 or 3 pairs of teeth are always in contact.   Such as high contact ratio generally is not obtained with external spur gears, but can be developed in the meshing of an internal and external spur gear pair or specially designed non-standard external spur gears.

                   (Rgo2 - Rgb2 )1/2 + (Rpo2 - Rpb2 )1/2  -  a sin α 
contact ratio m =                                                                   
        p cos α 

R _go = D _go / 2..Radius of Outside Dia of Gear
R _gb = D _gb / 2..Radius of Base Dia of Gear
R _po = D _po / 2..Radius of Outside Dia of Pinion
R _pb = D _pb / 2..Radius of Base Dia of Pinion
p = circular pitch.
a = ( d _g+ d _p )/2 = center distance. 

 Spur gear Forces, torques, velocities & Powers

F = tooth force between contacting teeth (at angle pressure angle α to pitch line tangent. (N) F t = tangential component of tooth force (N) F s = Separating component of tooth force α= Pressure angle d 1 = Pitch Circle Dia -driving gear (m) d 2 = Pitch Circle Dia -driven gear (m) ω 1 = Angular velocity of driver gear (Rads/s) ω 2 = Angular velocity of driven gear (Rads/s) z 1 = Number of teeth on driver gear z 2 = Number of teeth on driven gear P = power transmitted (Watts) M = torque (Nm) η = efficiency

Tangential force on gears F t = F cos α

Separating force on gears F s = F t tan α

Torque on driver gear T 1 = F t d 1 / 2

Torque on driver gear T 2 = F t d 2 / 2

Speed Ratio =ω 1 / ω 2 = d 2 / d 1 = z 2 /z 1

Input Power P 1 = T1 .ω 1

Output Power P 2 =η.T 1 .ω 2

 Spur gear Strength and durability calculations

Designing spur gears is normally done in accordance with standards the two most popular series are listed under standards above:

The notes below relate to approximate methods for estimating gear strengths. The methods are really only useful for first approximations and/or selection of stock gears (ref links below). — Detailed design of spur and helical gears is best completed using the standards.   Books are available providing the necessary guidance.   Software is also available making the process very easy.   A very reasonably priced and easy to use package is included in the links below (Mitcalc.com)

The determination of the capacity of gears to transfer the required torque for the desired operating life is completed by determining the strength of the gear teeth in bending and also the durability i.e of the teeth ( resistance to wearing/bearing/scuffing loads ) .. The equations below are based on methods used by Buckingham..

---

Bending

The basic bending stress for gear teeth is obtained by using the Lewis formula

σ = F_t / ( b_a. m. Y )

• F _t = Tangential force on tooth
• σ = Tooth Bending stress (MPa)
• b _a = Face width (mm)
• Y = Lewis Form Factor
• m = Module (mm)

Note: The Lewis formula is often expressed as

σ = F_t / ( b_a. p. y )

Where y = Y/π and p = circular pitch

When a gear wheel is rotating the gear teeth come into contact with some degree of impact.  To allow for this a velocity factor ( K_v ) is introduced into the equation.   This is given by the Barth equation...

V = the pitch line velocity = d.ω/2 (m/s)

The Lewis formula is thus modified as follows

σ = K _v.F_t / ( b_a. m. Y )

 

 Design Process
To select gears from a stock gear catalogue or do a first approximation for a gear design select the gear material and obtain a safe working stress e.g Yield stress / Factor of Safety. /Safe fatigue stress

• Determine the input speed, output speed, ratio, torque to be transmitted
• Select materials for the gears (pinion is more highly loaded than gear)
• Determine safe working stresses (uts /factor of safety or yield stress/factor of safety or Fatigue strength / Factor of safety )
• Determine Allowable endurance Stress S_e
• Select a module value and determine the resulting geometry of the gear
• Use the lewis formula and the endurance formula to establish the resulting face width
• If the gear proportions are reasonable then - proceed to more detailed evaluations
• If the resulting face width is excessive - change the module or material or both and start again

The gear face width should be selected in the range 9-15 x module or for straight spur gears-up to 60% of the pinion diameter.

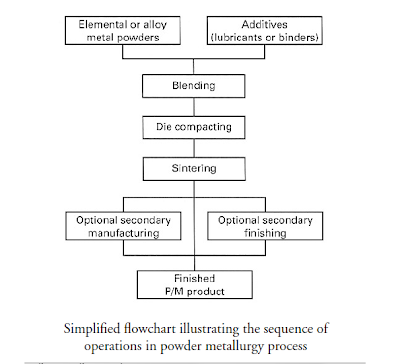
POWDER METALLURGY PROCESS

Overview

High quality gears can be made by Powder metallurgy method.Powder is pressed in dies to produce the tooth shape after which the product is sintered .This method is generally used for small gears .After the metallic powders have been produced and classified, the conventional P/M process sequence

consists of three major steps: (1) blending and mixing of powders, (2) compaction, and (3) sintering, and a number of optional and finishing secondary operations.

Blending and mixing

Blending: mixing powder of the same chemical composition but different sizes

Mixing: combining powders of different chemistries

Blending and mixing are accomplished by mechanical means:

Except for powders, some other ingredients are usually added:

1.  Lubricants: to reduce the particles-die friction
2. Binders: to achieve enough strength before sintering
3. Deflocculants: to improve the flow characteristics during feeding

Compaction

Blended powers are pressed in dies under high pressure to form them into the required shape. The

work part after compaction is called a green compact or simply a green, the word green meaning not

yet fully processed.

Sintering

Compressed metal powder is heated in a controlled-atmosphere furnace to a temperature below its

melting point, but high enough to allow bounding of the particles:

The primary driving force for sintering is not the fusion of material, but formation and growth of bonds

between the particles, as illustrated in a series of sketches showing on a microscopic scale the changes

that occur during sintering of metallic powders.

Finishing operations

A number of secondary and finishing operations can be applied after sintering, some of them are:

1. Sizing: cold pressing to improve dimensional accuracy
2. Coining: cold pressing to press details into surface
3. Impregnation: oil fills the pores of the part
4. Infiltration: pores are filled with a molten metal
5. Heat treating, plating, painting

Manufacturing Advantages of Powder Metallurgy:

• Cost Savings of up to 70% over other part manufacturing processes.
• Provides Close Dimensional Tolerances.
• Requires Minimal Machining.
• Results in Good Surface Finish.
• Excellent part to part reproducibility (Repetitive Accuracy).
• Often only process that produces parts with irregular curves, eccentrics, radial projections.
• Easily Produces parts requiring irregular holes, key-ways, flat sides, splines, or square holes.
• Easily Produces tapers and counter bores.
• Easily Produces slots, grooves, and bosses of varying depths.
• Axial projections possible but size depends on powder flowing into die recesses.
• Greater Customization Possible over other processes.
• Stronger Material Properties over plastics & dies casting.
• Greater Control of Material through sintering process, which is particularly important when working with stainless steel.
• Tailor material to be Ductile or Hard.
• Blend Materials to gain Desirable Material Properties.
• Corrosion Resistant.